1.三次方程的代数解法
意大利数学家卡达尔诺发现了三次方程的代数解法。不失一般性我们可以将三次代数方程写成：
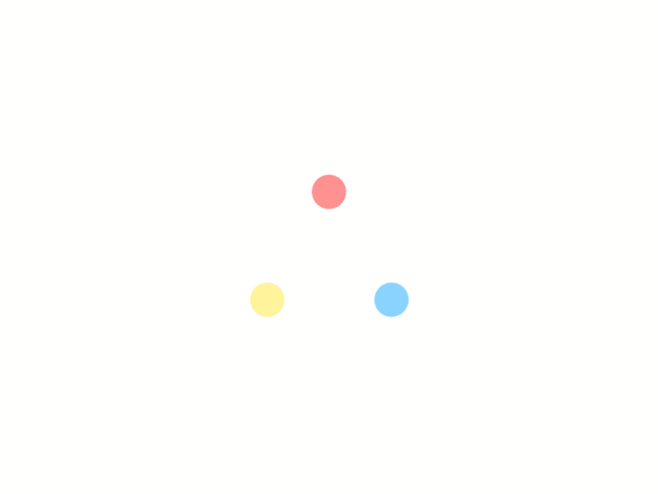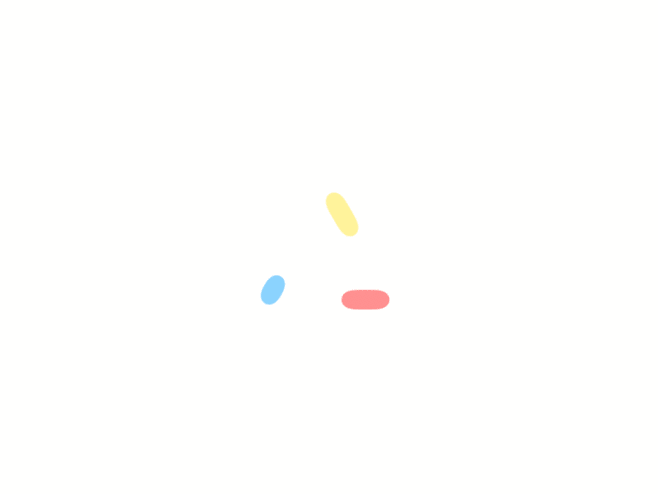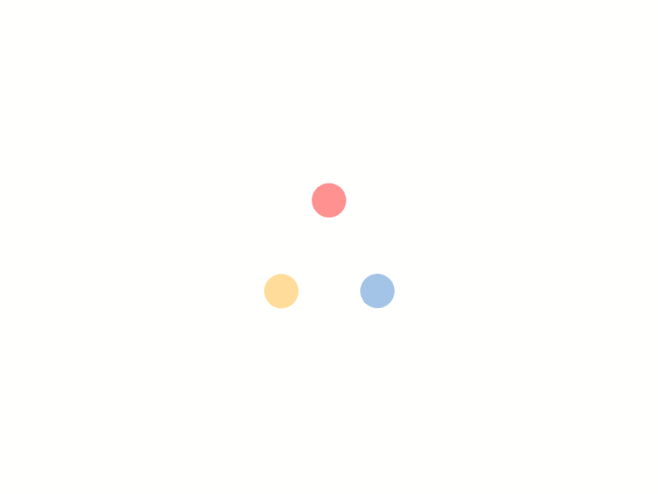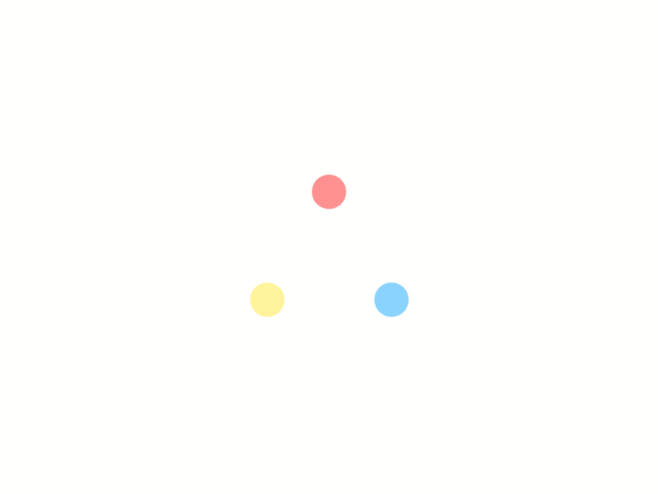
只要找到(1)的代数解，我们就找到了一般三次方程的代数解了。三次方程的解显然会是带开三次方的式子，我们假设（1）的解为：
三次方程成功地解出之后，卡尔达诺的学生费拉里受到启发给出了四次方程的代数解法。我有四次方程解法的完整推导过程，但太长，怕这种满是公式的文章没人看，就略去了。
2.解三次方程到复数
一元二次方程ax2+bx+c=0的根式解，只要判别式b2-4ac<0,我们认为是无解的，这并不构成什么障碍，二次方程通用解法发明后的1000多年里，人们并没感觉到不适应，毕竟负数的平方也是正数嘛。但到了三次方程就不一样了。
这样就在三次方程的代数解中出现了必须被正视的负数开平方的问题。卡达尔诺发现了三次方程的代数解法的同时，也发现了必须引入复数。他这样写到：
他已经懂得形式推导，但是获得的结果与传统观念差异太大，他不敢再前进一步，没有建立起复数的理论体系。
3.复数的符号i的建立过程
经过两百年左右的实践，欧拉确定了可以像对待实数运算那样那样看待虚数，而由高斯引入一个虚数符号
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容，请发送邮件至624739273@qq.com举报，一经查实，本站将立刻删除。
